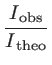In diffraction limited mode with adaptive optics the PSF is approximately composed of two functions:
- The core: This is an airy function of the telescope
- The halo: It is given by a Moffat function
IMoffat(r) = I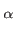 , ,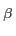 (r) = (r) = 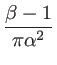 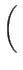 1 + 1 + 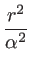 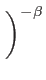 |
(7) |
I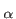 , ,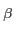 (r) (r) |
: |
Intensity at the distance r with parameters 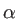 and and 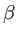 |
 |
: |
Parameter is used to fix the FWHM for a given 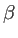 |
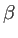 |
: |
Parameter to fix the amount of light in the lobes |
| r |
: |
Distance to the center
(r = 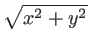 ) ) |
| FWHM |
: |
2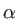  |
An example of such combined PSF is shown in Figure 1.
Figure 1:
Simplified description of an observed AO-PSF: It is built by a core (Airy function) and a halo (Moffat function).
|
![\includegraphics[width=0.77\textwidth]{pictures/psf_ao}](img61.png) |
For comparing the peak intensity of an ideal diffraction-limited optical system with a real system the Strehl parameter was introduced.
Strehl = 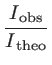 |
(8) |
This parameter is the ratio of the observed peak intensity at the detection plane of a telescope or other imaging system from a point source compared to the theoretical maximum peak intensity of a perfect imaging system working at the diffraction limit. For calculating the fraction of the halo and core component to achieve a certain strehl ratio the parameter F0 is introduced in this ETC. It has to fulfill the following equation:
In this mode the SNR is calculated for a disk with a radius of twice the radius of the airy disk.
Andre Germeroth
2016-11-04
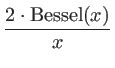
![\includegraphics[width=0.77\textwidth]{pictures/psf_ao}](img61.png)