Next: The Telescope Up: The Exposure-Time-Calculator Previous: The Exposure-Time-Calculator
| F0 | : | flux density for Vega at
|
|
F0 = 3.56 . 10-11 |
||
| mag | : | magnitude of the object |
| QE | : | quantum efficiency of the detector |
| T atm | : | transmission of the atmosphere |
| T tel | : | transmission of the telescope |
| T inst | : | transmission of the instrument (without any filter and grating) |
| T filt | : | transmission of the filter used |
| Observing mode | point source | extended source |
| Imaging |
|
|
| Spectroscopy |
|
|
| N | : | number of photons |
|
: | filter band width | |
| P | : | energy of one photon |
|
: | spectral resolution | |
| S | : | light-collecting area |
|
: | scale in imaging mode | |
| : | exposure time |
|
: | scale in spectroscopy mode |
In the near-infrared regime the SNR for the exposure time DIT is given by the formula:
| DARK DIT | : | dark current for 1 DIT |
| n pix | : | number of integration pixels1 |
| Nsky | : | sky signal for 1 DIT |
| RON | : | readout noise |
| SNRDIT | : | signal-to-noise ratio for 1 DIT |
In imaging mode the user will be asked for the signal-to-noise ratio for the exposure time ![]() (
SNR
(
SNR![]() ). The ETC calculates the necessary exposure time to achieve this
SNR
). The ETC calculates the necessary exposure time to achieve this
SNR![]() (see also formula 3):
(see also formula 3):
| = | NDIT . DIT and SNR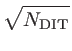 |
(4) | |
| = | 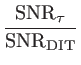 |
(5) |
| : | total exposure time | |
| DIT | : | detector integration time |
| NDIT | : | number of detector integrations |
|
SNR |
: | signal-to-noise ratio for exposure time |
| SNRDIT | : | signal-to-noise ratio for one DIT |
| SNR | : | signal-to-noise ratio for an exposure time of 1sec |
Andre Germeroth 2016-11-04